Iniciemos hablando sobre ¿qué es la geometría?

La geometría, una rama fundamental de las matemáticas que estudia las propiedades y las relaciones del espacio, las figuras y las formas.

Desde tiempos antiguos, la geometría ha sido una herramienta crucial para comprender el mundo que nos rodea, desde la disposición de los objetos en el espacio hasta la estructura de las moléculas en la naturaleza.

En este artículo, explicaremos los conceptos básicos de la geometría y cómo pueden ser abordados de manera efectiva para un aprendizaje sólido y progresivo.

¿Cómo aprender geometría desde cero?

La geometría trata de la medición y de las propiedades de puntos, líneas, ángulos, planos y sólidos, así como de las relaciones que guardan entre sí. A continuación veremos algunos conceptos relacionados con la geometría.


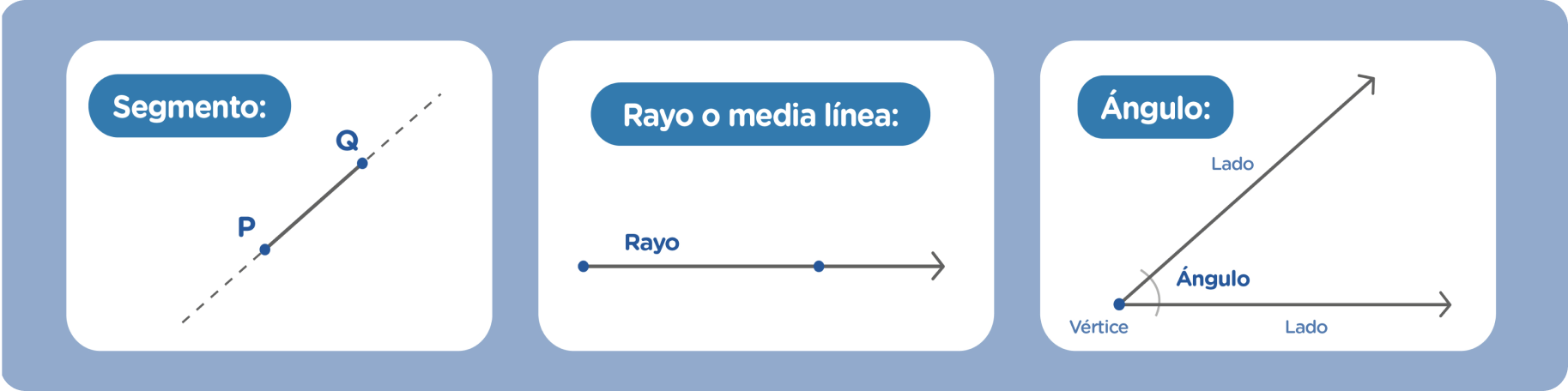
Segmento: es aquella parte de una línea recta que queda entre dos puntos señalados sobre ella.

Rayo o media línea: es aquella parte de una línea recta que queda en algún lado de un punto (el extremo) señalado sobre ella.

Ángulo: cuando dos rayos se intersectan en sus extremos. El punto de intersección se conoce con el nombre de vértice del ángulo.

En geometría, los ángulos son elementos fundamentales que se utilizan para medir la abertura entre dos líneas o segmentos de líneas que se cruzan en un punto común. Existen varios tipos de ángulos, cada uno con características específicas.


También puedes aumentar tus conocimientos con: Lo que debes saber sobre los monomios y polinomios.

Algunos ejemplos de geometría:

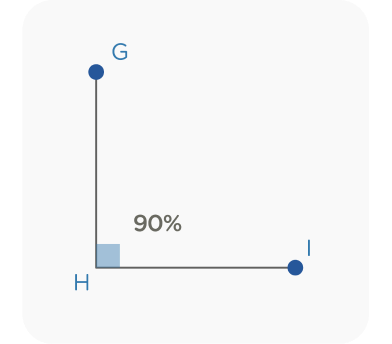
Ángulo recto: Se forma cuando dos rectas perpendiculares se cruzan, creando una apertura de 90 grados, que equivale a la cuarta parte de una vuelta completa.






Ángulo obtuso: Este tipo de ángulo tiene una apertura mayor que el ángulo recto, midiendo exactamente 180 grados.







Ángulo agudo: Los ángulos agudos tienen una apertura menor que el ángulo recto.






Ángulo plano: Se caracteriza por tener lados que son semirrectas opuestas y su apertura es de 180 grados, equivalente a la mitad de una vuelta completa.

¿Qué son los polígonos en geometría?

Por otra parte, los polígonos son figuras geométricas planas que están delimitadas por segmentos de recta llamados lados.


Se encuentran presentes en diversas aplicaciones en la vida cotidiana y en disciplinas como la arquitectura, la ingeniería y las ciencias naturales.

Estas figuras poseen características y propiedades particulares que las distinguen entre sí, como el número de lados, la longitud de los lados, los ángulos internos y la simetría.

Comprender los polígonos es esencial para entender conceptos más avanzados de geometría y para resolver una amplia variedad de problemas matemáticos y prácticos.

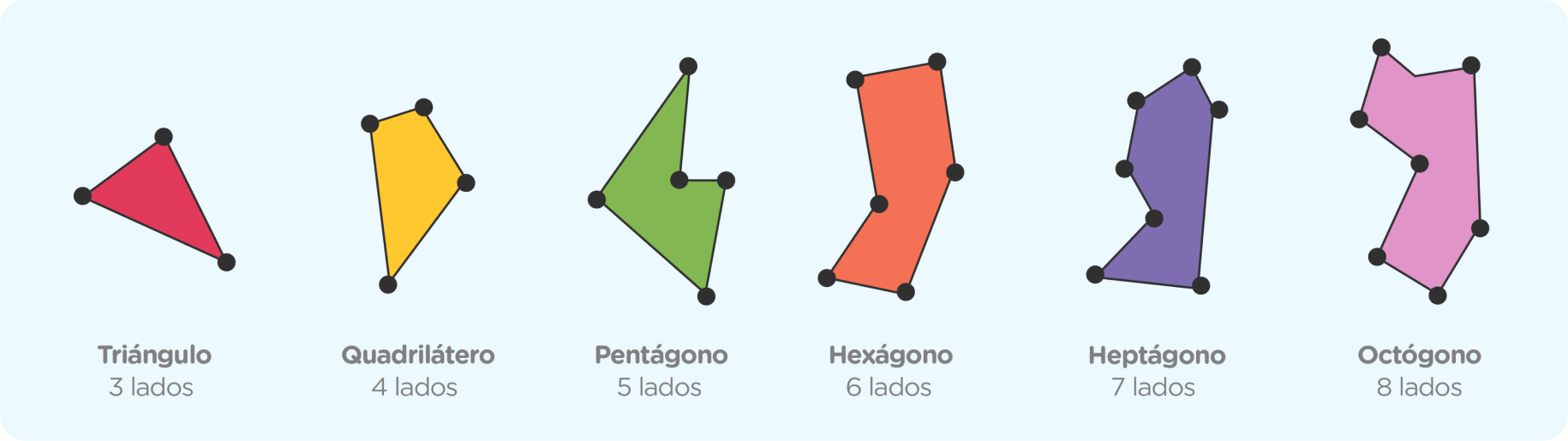
Existen diferentes tipos de polígonos como:

Polígonos regulares: son aquellos que tienen todos sus lados y ángulos congruentes. Además, todo polígono regular está inscrito en una circunferencia.


Polígono irregular: son aquellos que no tienen todos sus lados y ángulos iguales.

¡Ayuda a tu hijo a alcanzar su máximo potencial en matemáticas! Descubre cómo puedes marcar la diferencia en su educación y futuro fortaleciendo su capacidad para interpretar datos, desarrollar pensamiento lógico, comunicar ideas de manera efectiva y enfrentar desafíos con confianza.

Clases de figuras geométricas con nombre.

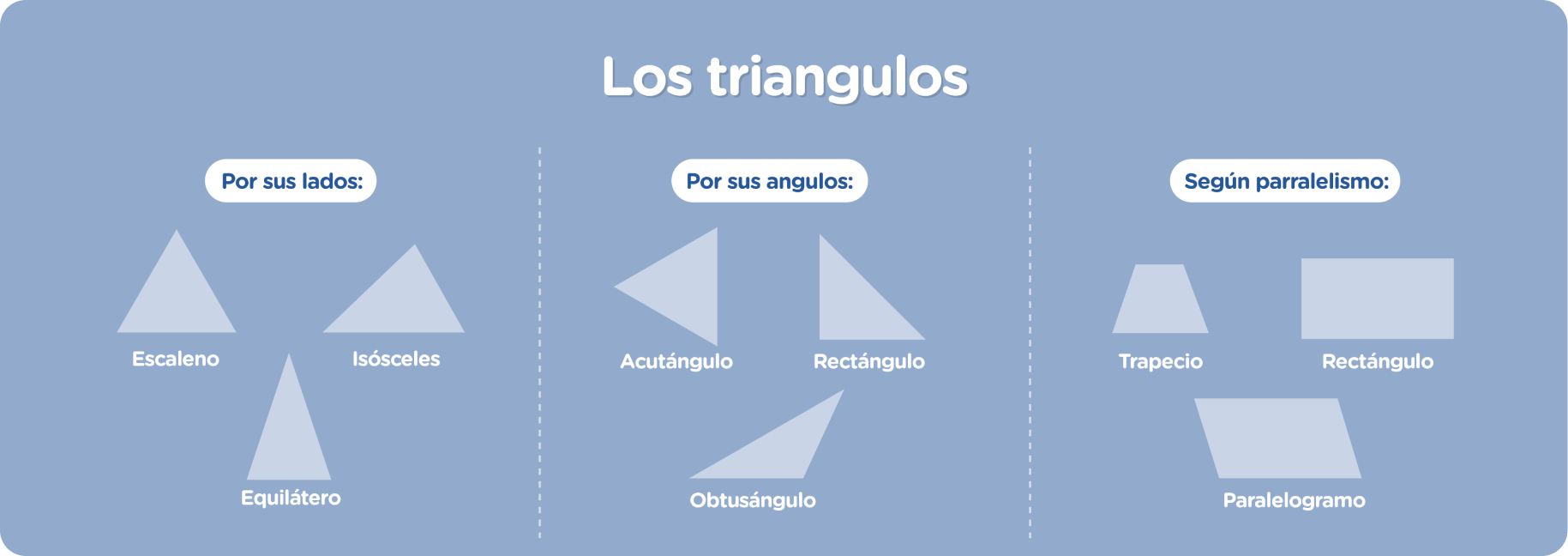
Los triángulos: son unos polígonos que tienen tres lados, que se unen en los vértices, y tres ángulos.
Los triángulos se pueden clasificar por do aspectos:

• Por sus lados:

Escaleno: sus lados y sus ángulos no son congruentes.
Isósceles: es un tipo de triángulo que tiene dos lados iguales. Los ángulos opuestos a estos lados iguales serán iguales.
Equilátero: es un triángulo que tiene sus tres lados iguales y sus ángulos también son iguales.

• Por sus ángulos:

Acutángulo: un triángulo acutángulo tiene sus tres ángulos agudos.
Obtusángulo: este tipo de triángulo tiene un ángulo obtuso y dos agudos. El lado opuesto al ángulo obtuso será de mayor longitud.
Rectángulo: es aquel triángulo que tiene un ángulo recto y dos agudos. El lado opuesto al ángulo recto se llama hipotenusa y los otros dos lados se llaman catetos.
Cuadriláteros: Un cuadrilátero es un polígono que tiene cuatro lados y cuatro ángulos. Los lados de un cuadrilátero pueden ser consecutivos u opuestos.

De acuerdo a la igualdad o al paralelismo de sus lados también podemos clasificarlos en:

• Según paralelismo:

Trapecio: El trapecio es un polígono de cuatro lados, pero sus cuatro ángulos son distintos de 90º.
Paralelogramo: El paralelogramo es un polígono de cuatro lados paralelos dos a dos.
Rectángulo: El rectángulo es un polígono de cuatro lados, iguales dos a dos. Sus cuatro ángulos son de 90 grados cada uno.


Aprende también: ¿Qué son los números romanos?

• Según la igualdad:

Romboide: tiene dos pares de lados consecutivos iguales.
Rombo: El rombo es un polígono de cuatro lados iguales, pero sus cuatro ángulos son distintos de 90ª.

La suma de todos los ángulos interiores de todo cuadrilátero es de 360º. El cuadrado puede situarse en ambas categorías.

¿Qué es PI en la geometría?

El número PI es un factor fundamental para medir el perímetro del círculo y a partir de ello se puede encontrar en los cálculos de herramientas que usamos hoy en día como el celular, el gps, los relojes, entre otros.

Para saber cuánto vale PI en geometría, debes dividir el perímetro de una circunferencia entre su diámetro. Este cociente siempre da como resultado el número π: 3,14… En su versión corta, ya que es un dígito irracional y tiene un número infinito de decimales.

Cuando dominas este tema será más fácil tener técnicas para enseñar geometría en secundaria o en el grado escolar en el que se encuentre tu hijo.


Antes de finalizar conoce: Unidades, decenas y centenas, ¿qué son?


En Kumon, el aprendizaje de la geometría comienza con la exploración de las formas básicas, como los cuadrados, triángulos y círculos.
A medida que los estudiantes avanzan, se introducen en conceptos más complejos, como los polígonos, los ángulos y las propiedades de las figuras bidimensionales y tridimensionales.

Nuestro enfoque se centra en la comprensión conceptual, permitiendo a los estudiantes no solo memorizar fórmulas y definiciones, sino también comprender el significado detrás de ellas.

Una de las características distintivas de Kumon es nuestro enfoque en la práctica repetitiva y gradual. A medida que los alumnos avanzan a través de nuestros cuadernillos, se enfrentan a una amplia variedad de ejercicios diseñados para reforzar y consolidar su comprensión de los conceptos de geometría.

En resumen, en Kumon, creemos que el aprendizaje de la geometría va más allá de simplemente memorizar fórmulas y teoremas.
Se trata de explorar, descubrir y comprender el fascinante mundo de las formas y las figuras, y de desarrollar habilidades matemáticas fundamentales que servirán a los estudiantes en su vida académica y más allá.

 ¡Agenda ahora una prueba de diagnóstico gratuita en Kumon y descubre cómo tu hijo puede generar gusto por aprender al tiempo que desarrolla habilidades en lógica y autonomía con Kumon Matemáticas!