¿Alguna vez te has preguntado cómo representar los números de una manera visual y fácil de entender? Pues la recta numérica es la respuesta.

En este artículo, conocerás qué es la recta numérica, sus características, usos en la vida cotidiana, un poco de su historia y algunos ejercicios para practicar en casa.

¿Cuál es la definición de la recta numérica?

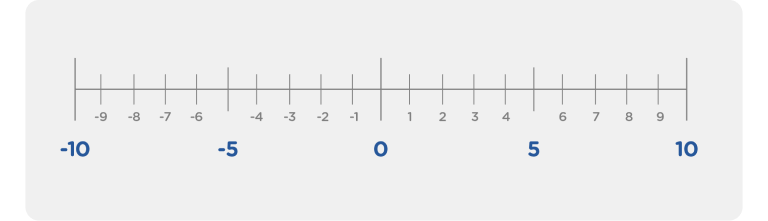
La recta numérica es una línea horizontal en la que se representan los números de forma ordenada y equidistante. 

Generalmente, comienza con el cero y se extiende hacia la derecha de forma infinita, representando los números positivos y hacia la izquierda para los números negativos.

Cada punto en la línea representa un número entero y la distancia entre cada número es la misma, lo cual ayuda a los niños a visualizar la progresión de los números y comprender su orden.

La recta numérica es una representación gráfica que muestra los números en una línea horizontal. Cada punto en la línea corresponde a un número, y la distancia entre los puntos es igual, lo que refleja la relación de orden entre los números.

La recta numérica se extiende infinitamente en ambas direcciones, mostrando tanto los números positivos como los negativos y el cero en el centro.

Características de la recta numérica.

Linealidad: la recta numérica es una línea recta continua, sin fin, en ambas direcciones.



Punto de origen: el cero se coloca en el centro y sirve como punto de referencia.



Equidistancia: los puntos que representan los números están equidistantes entre si.



Bidireccionalidad: se extiende hacia la derecha para los números positivos y hacia la izquierda para los números negativos.



Inclusividad: puede incluir cualquier tipo de número: naturales, enteros, racionales, irracionales y reales.



Conoce también: Lo que debes saber sobre los monomios y polinomios.

Importancia de la recta numérica en el aprendizaje

La recta numérica es crucial por varias razones:

• Visualización de la secuencia numérica: tus hijos pueden entender que los números aumentan a la derecha y disminuyen a la izquierda.

• Operaciones matemáticas básicas: facilita la comprensión de sumas y restas. Por ejemplo, sumar 2 al número 3 implica mover dos espacios hacia la derecha en la recta.

• Introducción a conceptos avanzados: a medida que los niños crecen, la recta numérica puede ampliarse para incluir números negativos, fracciones y decimales, ayudándolos a entender conceptos más complejos.

¿Cómo enseñarle a tu hijo a clasificar los números en una recta numérica con ejemplos?

Comienza con los números más básicos, los números naturales (N) que son los que utilizamos para contar.

Para ubicarlos en la recta numérica, primero marcamos un punto en la recta y lo denominamos 0 luego, dividimos la recta en segmentos de igual longitud.

Cada segmento representa una unidad, separando un número entero del siguiente. De esta manera:

• Marcamos el punto 0 en la recta
• Dividimos la recta en segmentos iguales a partir del punto 0
• Los números naturales se ubican a la derecha del 0

Ubicación de números enteros (Z) en la recta numérica.

Los números enteros (Z) incluyen tanto los números naturales como sus opuestos negativos. Su representación en la recta es de la misma forma que los naturales, pero extendiendo la numeración en ambos sentidos a partir del 0 así:

• Dividimos la recta en segmentos iguales, con el punto 0 en el centro
• Los números enteros positivos se ubican a la derecha del 0
• Los números enteros negativos se ubican a la izquierda del 0

En Kumon Matemáticas tus hijos descubren el amplio universo de las matemáticas a la vez que desarrollan habilidades como la lógica y agilidad mental, esenciales para el desarrollo del futuro profesional.

Ubicación de números racionales (Q) en la recta numérica

Los números racionales (Q) abarcan a los enteros y naturales e incluyen también los números que pueden expresarse como fracciones o decimales. Para ubicarlos en la recta numérica:

• El denominador de la fracción indica en cuántas partes iguales se debe dividir cada segmento de la unidad
• El numerador muestra en cuál de esos puntos se localiza el número  
• Si el número es positivo, se ubica a la derecha del 0
• Si es negativo, se ubica a la izquierda del 0

Por ejemplo, para ubicar 3/4 en la recta numérica, dividimos el segmento entre 0 y 1 en cuatro partes iguales y contamos tres partes hacia la derecha del 0. Para -3/4, haríamos lo mismo pero hacia la izquierda del 0 así:

• Dividimos la recta en segmentos iguales y fracciones de estos segmentos
• Ubicamos los números racionales según sus fracciones positivas o negativas a la derecha o izquierda del 0, respectivamente

Utilidades de la recta numérica en la vida cotidiana

La recta numérica es más que una herramienta matemática; tiene múltiples aplicaciones prácticas en la vida diaria:

Educación: es fundamental para enseñar conceptos básicos de aritmética y álgebra.

Finanzas: ayuda a entender pérdidas y ganancias, balance de cuentas y cálculo de intereses.

Mediciones: facilita la comprensión de escalas y proporciones en diversas disciplinas como la física y la química.

Geografía: se utiliza en la representación de coordenadas y la ubicación de lugares en un mapa.

Planificación y organización: permite visualizar cronogramas y secuencias de eventos.


Antes de terminar la lectura enséñale a tu hijo sobre: ¿Qué son los números romanos?

10 ejercicios para que tu hijo aprenda más sobre la recta numérica.

1. Ubicación de números naturales:
Marca los siguientes números naturales en una recta numérica: 2, 5, 7, 10, 13.

2. Ubicación de números enteros:
Dibuja una recta numérica y ubica los siguientes números enteros: -3, -1, 0, 2, 4, 6.

3. Ubicación de números racionales:
Coloca los siguientes números racionales en la recta numérica: 1/2, 3/4, -1/3, -5/6.

4. Identificación de puntos:
Dibuja una recta numérica y marca los puntos -2, 0, y 3. Luego, escribe cuál es la distancia entre cada par de puntos.

5. Fracciones en la recta numérica:
Ubica las siguientes fracciones en la recta numérica: 2/3, -3/4, 5/8, -7/8.

6. Sumas y restas en la recta numérica:
Utiliza una recta numérica para resolver las siguientes operaciones y marca los resultados:


7. Multiplicación y división en la recta numérica:
Dibuja una recta numérica y utiliza segmentos para mostrar las siguientes multiplicaciones y divisiones:


8. Decimales en la recta numérica:
Coloca los siguientes números decimales en la recta numérica: 0.5, -1.2, 3.75, -0.25. 9.

9. Encuentra el número faltante:
Dibuja una recta numérica y marca los puntos -5, -3, __, 1, 3. Encuentra el número faltante.

10. Compara números en la recta numérica:
Dibuja una recta numérica y coloca los números 2, -4, 1/2, -3/4. Luego, escribe cuál es el mayor y el menor de estos números.

¿Cómo aprende tu hijo en Kumon?

En Kumon, la recta numérica es una herramienta fundamental que ayuda a los alumnos a comprender los números de una manera visual y práctica. 

A través de este recurso, tus hijos pueden ver cómo se organizan los números en una línea, comprendiendo las relaciones de orden y magnitud entre ellos. 

Pero en Kumon vamos más allá de solo enseñar qué es la recta numérica, utilizamos esta herramienta para desarrollar habilidades desde los niveles más básicos.

En las primeras etapas del método, los alumnos trabajan con la recta numérica para aprender a contar de forma progresiva. 

Este enfoque visual les permite reconocer patrones de forma más sencilla y entender, por ejemplo, que al moverse hacia la derecha en la recta los números aumentan y que al moverse hacia la izquierda, disminuyen. Es una manera de hacer que el aprendizaje sea intuitivo y menos abstracto.

A medida que avanzan los alumnos comienzan a utilizar la recta numérica para resolver operaciones matemáticas, como la suma y la resta, entendiendo cómo el movimiento en la recta representa estas operaciones. 

Este tipo de ejercicios fortalece su sentido numérico, facilitando el aprendizaje de conceptos matemáticos más complejos en el futuro, como la multiplicación o el manejo de números negativos.

El método Kumon también enfatiza la práctica constante y el aprendizaje a su propio ritmo, lo que permite a cada alumno dominar la recta numérica sin presiones, ganando confianza y habilidades matemáticas esenciales. 

Gracias a esta base sólida, los niños no solo aprenden a operar con números, sino que desarrollan una comprensión profunda y duradera de las matemáticas que les acompañará en su camino académico.

El método Kumon logra que tu hijo domine la recta numérica, gracias a que realizan ejercicios diarios que refuerzan su comprensión de cómo ubicar diferentes tipos de números en la recta, desde números naturales y enteros hasta fracciones y decimales.

Esta práctica continua ayuda a consolidar su conocimiento y habilidades.

Agenda ahora una prueba de diagnóstico gratuita en Kumon y descubre cómo ayudar a tu hijo a que desarrolle el gusto por aprender Matemáticas.